what would be the best description of the johns times rounded to quarter hours

Lesson 10: Altitude Word Problems

/en/algebra-topics/introduction-to-give-and-take-problems/content/

What are distance word problems?

Distance word issues are a common type of algebra give-and-take bug. They involve a scenario in which y'all demand to figure out how fast, how far, or how long one or more objects have traveled. These are often called railroad train issues considering one of the near famous types of distance bug involves finding out when 2 trains heading toward each other cross paths.

In this lesson, you'll learn how to solve train problems and a few other mutual types of distance problems. Only first, allow's wait at some basic principles that employ to any altitude problem.

The basics of distance problems

There are 3 bones aspects to movement and travel: distance, rate, and fourth dimension. To understand the difference among these, call up nigh the last time you collection somewhere.

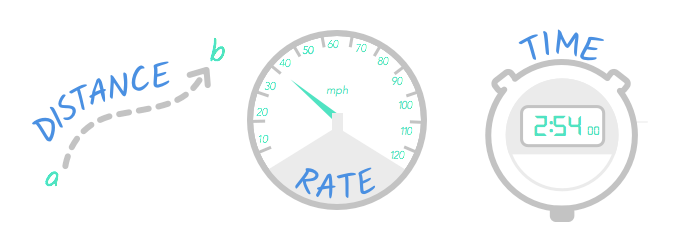
The distance is how far you traveled. The rate is how fast you traveled. The time is how long the trip took.

The relationship amid these things can be described by this formula:

distance = rate x fourth dimension
d = rt

In other words, the distance you drove is equal to the rate at which you drove times the amount of time y'all drove. For an instance of how this would work in real life, just imagine your last trip was like this:

• You drove 25 miles—that'south the distance.
• You drove an average of l mph—that'south the rate.
• The drive took you 30 minutes, or 0.5 hours—that'southward the time.

Co-ordinate to the formula, if we multiply the charge per unit and time, the product should be our distance.

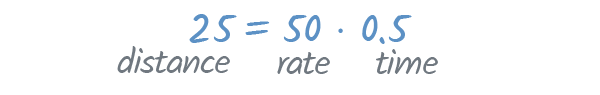
And it is! We collection l mph for 0.5 hours—and fifty ⋅ 0.v equals 25, which is our distance.

What if nosotros collection 60 mph instead of 50? How far could we drive in 30 minutes? Nosotros could employ the same formula to figure this out.

60 ⋅ 0.5 is thirty, then our distance would be 30 miles.

Solving altitude problems

When y'all solve any distance trouble, you'll have to do what we simply did—utilise the formula to detect distance, rate, or time. Let's attempt another simple trouble.

On his day off, Lee took a trip to the zoo. He collection an boilerplate speed of 65 mph, and it took him two-and-a-half hours to go from his house to the zoo. How far is the zoo from his firm?

First, we should identify the information we know. Recall, we're looking for any information about distance, rate, or time. According to the problem:

• The charge per unit is 65 mph.
• The fourth dimension is two-and-a-half hours, or 2.v hours.
• The distance is unknown—it's what we're trying to find.

You could flick Lee's trip with a diagram like this:

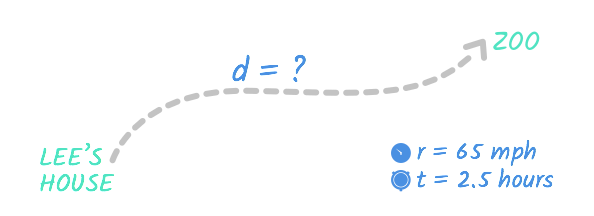
This diagram is a starting time to understanding this problem, but we even so have to figure out what to do with the numbers for distance, rate, and time. To continue track of the information in the trouble, nosotros'll set up a table. (This might seem excessive at present, merely it's a good habit for fifty-fifty simple problems and tin can make solving complicated problems much easier.) Here's what our table looks like:

distance	rate	fourth dimension
d	65	2.5

We can put this data into our formula: distance = rate ⋅ time.

Nosotros tin use the altitude = rate ⋅ time formula to discover the distance Lee traveled.

d = rt

The formula d = rt looks like this when nosotros plug in the numbers from the problem. The unknown altitude is represented with the variable d.

d = 65 ⋅ 2.five

To find d, all we take to practice is multiply 65 and 2.5. 65 ⋅ 2.five equals 162.5.

d = 162.five

We have an reply to our problem: d = 162.five. In other words, the distance Lee drove from his house to the zoo is 162.v miles.

Be careful to employ the same units of measurement for rate and time. Information technology's possible to multiply 65 miles per hour past two.five hours because they use the same unit of measurement: an hour. However, what if the time had been written in a unlike unit, like in minutes? In that case, you'd accept to catechumen the time into hours so it would use the same unit as the rate.

Solving for rate and fourth dimension

In the trouble nosotros just solved nosotros calculated for distance, but you can utilise the d = rt formula to solve for charge per unit and time too. For example, take a look at this problem:

Subsequently work, Janae walked in her neighborhood for a half hour. She walked a mile-and-a-half total. What was her average speed in miles per hour?

We tin picture Janae's walk as something similar this:

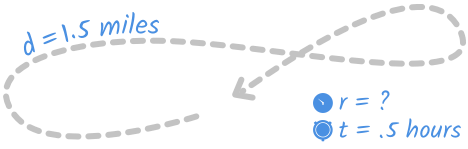
And nosotros tin can fix the information from the trouble we know similar this:

distance	rate	time
1.v	r	0.5

The tabular array is repeating the facts nosotros already know from the trouble. Janae walked 1-and-a-half miles or ane.5 miles in a half hour, or 0.v hours.

As always, we kickoff with our formula. Next, we'll fill in the formula with the information from our table.

d = rt

The charge per unit is represented by r because we don't yet know how fast Janae was walking. Since we're solving for r, nosotros'll take to get it lone on one side of the equation.

1.five = r ⋅ 0.five

Our equation calls for r to be multiplied by 0.5, so nosotros can get r alone on one side of the equation by dividing both sides by 0.5:
i.5 / 0.5 = 3.

3 = r

r = 3, and so iii is the respond to our trouble. Janae walked 3 miles per hr.

In the bug on this page, we solved for distance and rate of travel, just you lot can also use the travel equation to solve for time. You tin fifty-fifty use information technology to solve certain issues where you're trying to figure out the distance, rate, or time of two or more moving objects. We'll expect at bug like this on the adjacent few pages.

Two-part and round-trip problems

Do you lot know how to solve this problem?

Neb took a trip to run into a friend. His friend lives 225 miles away. He drove in boondocks at an average of thirty mph, then he drove on the interstate at an average of 70 mph. The trip took 3-and-a-half hours total. How far did Beak bulldoze on the interstate?

This problem is a classic two-part trip trouble because it'due south request you to find data near i role of a two-part trip. This problem might seem complicated, but don't be intimidated!

You lot tin can solve information technology using the aforementioned tools we used to solve the simpler problems on the first folio:

• The travel equation d = rt
• A tabular array to keep rails of important information

Let'due south start with the table. Accept another look at the problem. This time, the data relating to altitude, rate, and time has been underlined.

Bill took a trip to encounter a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, and so he collection on the interstate at an average of 70 mph. The trip took 3-and-a-one-half hours total. How far did Bill drive on the interstate?

If you lot tried to fill in the table the way nosotros did on the last page, you might have noticed a problem: There's too much information. For instance, the problem contains ii rates—xxx mph and 70 mph. To include all of this information, allow's create a table with an actress row. The top row of numbers and variables will be labeled in town, and the bottom row volition be labeled interstate.

	altitude	rate	time
in town		30
interstate		seventy

We filled in the rates, just what nearly the distance and time? If you await dorsum at the problem, yous'll see that these are the full figures, meaning they include both the time in boondocks and on the interstate. So the total distance is 225. This ways this is true:

Interstate distance + in-town distance = Total altitude

Together, the interstate distance and in-boondocks altitude are equal to the full distance. See?

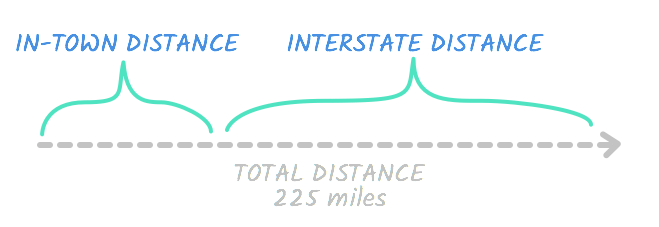
In any case, we're trying to find out how far Bill drove on the interstate, so let's represent this number with d. If the interstate altitude is d, it means the in-town distance is a number that equals the total, 225, when added to d. In other words, it's equal to 225 - d .

We can fill up in our chart like this:

	distance	rate	time
in town	225 - d	30
interstate	d	lxx

We can utilise the same technique to fill in the time column. The full time is 3.five hours. If we say the fourth dimension on the interstate is t, then the remaining time in boondocks is equal to 3.5 - t . We can fill in the rest of our chart.

	distance	rate	time
in boondocks	225 - d	30	3.five - t
interstate	d	70	t

Now we tin work on solving the problem. The primary departure betwixt the problems on the offset page and this problem is that this trouble involves two equations. Here's the 1 for in-town travel:

225 - d = 30 ⋅ (3.five - t)

And hither'southward the one for interstate travel:

d = 70t

If you tried to solve either of these on its ain, you might have found information technology impossible: since each equation contains ii unknown variables, they tin't exist solved on their own. Try for yourself. If yous piece of work either equation on its own, you won't be able to observe a numerical value for d. In order to find the value of d, nosotros'll also accept to know the value of t.

We tin can find the value of t in both bug by combining them. Let's have some other look at our travel equation for interstate travel.

While nosotros don't know the numerical value of d, this equation does tell us that d is equal to seventyt .

d = 70t

Since 70t and d are equal, we can supervene upon d with 70t . Substituting 70t for d in our equation for interstate travel won't help us find the value of t—all it tells the states is that seventyt is equal to itself, which we already knew.

70t = 70t

But what about our other equation, the 1 for in-boondocks travel?

225 - d = 30 ⋅ (3.5 - t)

When we supplant the d in that equation with 70t , the equation suddenly gets much easier to solve.

225 - 70t = 30 ⋅ (iii.five - t)

Our new equation might look more complicated, but information technology's really something we can solve. This is considering it only has one variable: t. One time nosotros notice t, we can utilise it to calculate the value of d—and detect the answer to our problem.

To simplify this equation and observe the value of t, we'll have to go the t solitary on ane side of the equals sign. Nosotros'll besides have to simplify the right side as much equally possible.

225 - 70t = 30 ⋅ (iii.5 - t)

Let's start with the right side: xxx times (iii.five - t) is 105 - 30t .

225 - 70t = 105 - 30t

Next, let'due south abolish out the 225 adjacent to 70t . To do this, we'll subtract 225 from both sides. On the right side, information technology means subtracting 225 from 105. 105 - 225 is -120.

- 70t = -120 - 30t

Our next step is to group like terms—think, our eventual goal is to take t on the left side of the equals sign and a number on the right. We'll cancel out the -30t on the correct side past adding 30t to both sides. On the right side, we'll add together information technology to -lxxt . -70t + 30t is -fortyt .

- 40t = -120

Finally, to get t on its ain, we'll split each side by its coefficient: -xl. -120 / - 40 is 3.

t = 3

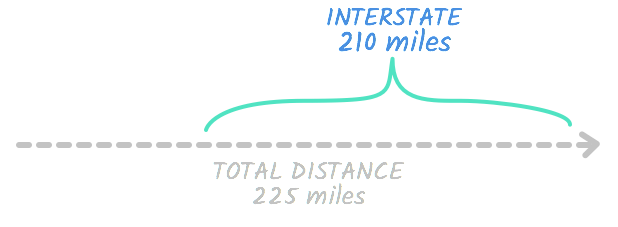
Then t is equal to 3. In other words, the time Nib traveled on the interstate is equal to iii hours. Recall, we're ultimately trying to discover the distanc e Neb traveled on the interstate. Let's wait at the interstate row of our chart once again and see if nosotros have plenty information to find out.

	distance	rate	time
interstate	d	70	3

It looks like nosotros exercise. Now that we're merely missing one variable, we should be able to notice its value pretty chop-chop.

To find the distance, we'll apply the travel formula distance = rate ⋅ time.

d = rt

We now know that Pecker traveled on the interstate for 3 hours at 70 mph, so nosotros can make full in this data.

d = 3 ⋅ 70

Finally, nosotros finished simplifying the correct side of the equation. 3 ⋅ lxx is 210.

d = 210

So d = 210. We accept the answer to our problem! The altitude is 210. In other words, Bill drove 210 miles on the interstate.

Solving a round-trip trouble

It might take seemed like it took a long time to solve the commencement problem. The more exercise you get with these issues, the quicker they'll go. Let'due south try a like problem. This i is called a round-trip problem because it describes a round trip—a trip that includes a return journey. Fifty-fifty though the trip described in this problem is slightly dissimilar from the one in our first problem, yous should be able to solve it the same way. Let'due south take a expect:

Eva drove to work at an average speed of 36 mph. On the mode abode, she striking traffic and but drove an boilerplate of 27 mph. Her total fourth dimension in the car was ane hour and 45 minutes, or 1.75 hours. How far does Eva live from work?

If you're having trouble understanding this problem, you lot might desire to visualize Eva'southward commute like this:

As ever, let'south start past filling in a tabular array with the important information. We'll make a row with information nigh her trip to work and from piece of work.

1.75 - t to draw the trip from work. (Retrieve, the full travel time is 1.75 hours, and so the time to piece of work and from piece of work should equal i.75.)

From our tabular array, we tin write two equations:

• The trip to piece of work tin exist represented equally d = 36t .
• The trip from work can exist represented as d = 27 (1.75 - t).

In both equations, d represents the total distance. From the diagram, yous tin see that these two equations are equal to each other—subsequently all, Eva drives the same distance to and from work.

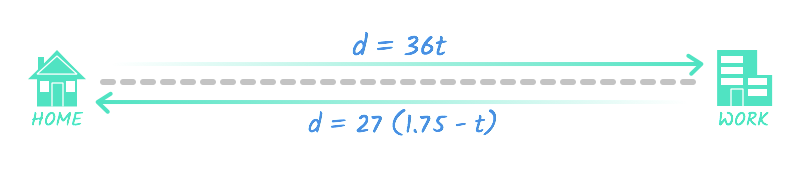
Just similar with the terminal problem we solved, nosotros can solve this i past combining the two equations.

We'll outset with our equation for the trip from piece of work.

d = 27 (1.75 - t)

Next, we'll substitute in the value of d from our to work equation, d = 36t . Since the value of d is 36t , nosotros can replace any occurrence of d with 36t .

36t = 27 (1.75 - t)

Now, permit's simplify the correct side. 27 ⋅(i.75 - t) is 47.25.

36t = 47.25 - 27t

Next, we'll cancel out -27t by adding 27t to both sides of the equation. 36t + 27t is 63t .

63t = 47.25

Finally, we tin can get t on its own past dividing both sides past its coefficient: 63. 47.25 / 63 is .75.

t = .75

t is equal to .75. In other words, the time information technology took Eva to drive to work is .75 hours. Now that nosotros know the value of t, we'll exist able to can find the distance to Eva's work.

If you guessed that nosotros were going to apply the travel equation again, you were right. We now know the value of ii out of the three variables, which ways we know plenty to solve our problem.

d = rt

Offset, allow'southward fill up in the values we know. Nosotros'll work with the numbers for the trip to piece of work. We already knew the rate: 36. And we but learned the time: .75.

d = 36 ⋅ .75

Now all we take to do is simplify the equation: 36 ⋅ .75 = 27.

d = 27

d is equal to 27. In other words, the distance to Eva's work is 27 miles. Our problem is solved.

Intersecting distance problems

An intersecting distance problem is 1 where two things are moving toward each other. Here'south a typical problem:

Pawnee and Springfield are 420 miles autonomously. A train leaves Pawnee heading to Springfield at the same fourth dimension a train leaves Springfield heading to Pawnee. One train is moving at a speed of 45 mph, and the other is moving sixty mph. How long will they travel before they meet?

This problem is asking you to calculate how long it will take these 2 trains moving toward each other to cantankerous paths. This might seem disruptive at first. Even though information technology's a real-earth situation, it can be difficult to imagine altitude and motion abstractly. This diagram might help you get a sense of what this situation looks like:

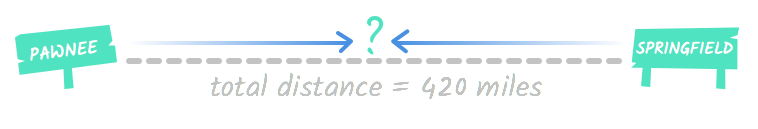
If you're yet confused, don't worry! You can solve this trouble the aforementioned mode you lot solved the 2-role issues on the last folio. You'll only need a chart and the travel formula.

Pawnee and Springfield are 420 miles autonomously. A train leaves Pawnee heading toward Springfield at the same fourth dimension a train leaves Springfield heading toward Pawnee. I train is moving at a speed of 45 mph, and the other is moving threescore mph. How long volition they travel before they meet?

Let's commencement past filling in our chart. Here's the problem again, this time with the important information underlined. Nosotros can start by filling in the most obvious information: rate. The problem gives us the speed of each railroad train. We'll characterization them fast railroad train and deadening train. The fast train goes 60 mph. The tiresome train goes only 45 mph.

Nosotros tin also put this information into a tabular array:

	distance	charge per unit	time
fast train		60
ho-hum train		45

We don't know the distance each train travels to meet the other yet—we just know the total distance. In club to meet, the trains will cover a combined distance equal to the total altitude. As yous can see in this diagram, this is true no matter how far each train travels.

This means that—merely like last time—we'll correspond the distance of one with d and the distance of the other with the total minus d. So the distance for the fast railroad train will be d , and the altitude for the slow train will be 420 - d .

	distance	rate	fourth dimension
fast railroad train	d	60
slow railroad train	420 - d	45

Because we're looking for the time both trains travel earlier they meet, the fourth dimension will be the same for both trains. We tin represent it with t.

	distance	rate	fourth dimension
fast railroad train	d	60	t
deadening train	420 - d	45	t

The tabular array gives united states two equations: d = 60t and 420 - d = 45t . Simply like nosotros did with the two-part issues, nosotros tin can combine these two equations.

The equation for the fast train isn't solvable on its ain, simply it does tell the states that d is equal to 60t .

d = 60t

The other equation, which describes the slow train, can't be solved alone either. Notwithstanding, we tin supervene upon the d with its value from the first equation.

420 - d = 45t

Because we know that d is equal to threescoret , nosotros tin replace the d in this equation with 60t . Now nosotros have an equation nosotros tin can solve.

420 - 60t = 45t

To solve this equation, we'll need to get t and its coefficients on one side of the equals sign and whatsoever other numbers on the other. Nosotros can commencement past canceling out the -sixtyt on the left past adding 60t to both sides. 45t + sixtyt is 105t .

420 = 105t

Now nosotros just need to get rid of the coefficient adjacent to t. We tin can exercise this by dividing both sides by 105. 420 / 105 is 4.

4 = t

t = 4. In other words, the time information technology takes the trains to meet is 4 hours. Our problem is solved!

If you want to be sure of your answer, you can check it by using the distance equation with t equal to iv. For our fast train, the equation would be d = 60 ⋅ iv. threescore ⋅ 4 is 240, then the distance our fast train traveled would be 240 miles. For our slow train, the equation would be d = 45 ⋅ 4. 45 ⋅ four is 180, and so the distance traveled by the slow train is 180 miles.

Recall how we said the distance the slow train and fast train travel should equal the total distance? 240 miles + 180 miles equals 420 miles, which is the total distance from our trouble. Our reply is correct.

Practice trouble 1

Hither's another intersecting distance problem. It's similar to the one nosotros just solved. Run across if you tin solve it on your ain. When yous're finished, scroll downwardly to come across the reply and an explanation.

Jon and Dani live 270 miles apart. One mean solar day, they decided to bulldoze toward each other and hang out wherever they met. Jon drove an boilerplate of 65 mph, and Dani drove an average of lxx mph. How long did they drive before they met upwards?

Trouble i answer

Here's practice trouble ane:

Jon and Dani alive 270 miles apart. One mean solar day, they decided to drive toward each other and hang out wherever they met. Jon drove an boilerplate of 65 mph, and Dani drove 70 mph. How long did they drive before they met upwardly?

Answer: 2 hours.

Let's solve this trouble like nosotros solved the others. Get-go, try making the chart. Information technology should look like this:

	distance	rate	time
Jon	d	65	t
Dani	270 - d	lxx	t

Here's how we filled in the nautical chart:

• Distance: Together, Dani and Jon will have covered the total distance betwixt them by the time they meet up. That'southward 270. Jon's distance is represented by d , so Dani's distance is 270 - d .
• Rate: The problem tells united states Dani and Jon'due south speeds. Dani drives 65 mph, and Jon drives 70 mph.
• Time: Considering Jon and Dani drive the same amount of time before they encounter upward, both of their travel times are represented by t.

Now we have two equations. The equation for Jon'southward travel is d = 65t . The equation for Dani's travel is 270 - d = 70t . To solve this problem, we'll need to combine them.

The equation for Jon tells the states that d is equal to 65t . This means we can combine the two equations by replacing the d in Dani's equation with 65t .

270 - 65t = 70t

Let'southward get t on one side of the equation and a number on the other. The first step to doing this is to get rid of -65t on the left side. We'll cancel it out by calculation 65t to both sides: 70t + 65t is 135t.

270 = 135t

All that'south left to exercise is to get rid of the 135 next to the t. Nosotros tin can practice this past dividing both sides by 135: 270 / 135 is ii.

2 = t

That's it. t is equal to 2. Nosotros have the answer to our trouble: Dani and Jon drove 2 hours earlier they met up.

Overtaking distance issues

The final type of distance problem we'll discuss in this lesson is a problem in which one moving object overtakes—or passes—some other. Here's a typical overtaking problem:

The Colina family unit and the Platter family unit are going on a road trip. The Hills left 3 hours before the Platters, but the Platters drive an average of 15 mph faster. If it takes the Platter family 13 hours to take hold of up with the Hill family, how fast are the Hills driving?

You can picture the moment the Platter family left for the road trip a little similar this:

The trouble tells united states of america that the Platter family will take hold of upwardly with the Loma family in thirteen hours and asks u.s. to apply this information to find the Hill family's charge per unit. Like some of the other problems we've solved in this lesson, it might not seem like we have enough information to solve this problem—but we do. Permit's start making our chart. The distance can exist d for both the Hills and the Platters—when the Platters catch upwardly with the Hills, both families will have driven the exact same distance.

	altitude	rate	fourth dimension
the Hills	d
the Platters	d

Filling in the charge per unit and fourth dimension will require a trivial more thought. We don't know the rate for either family—remember, that's what nosotros're trying to find out. Nevertheless, we do know that the Platters collection 15 mph faster than the Hills. This means if the Hill family'south rate is r , the Platter family's rate would be r + 15.

	altitude	rate	fourth dimension
the Hills	d	r
the Platters	d	r + 15

Now all that'south left is the time. Nosotros know information technology took the Platters 13 hours to catch upwards with the Hills. Nevertheless, remember that the Hills left 3 hours earlier than the Platters—which means when the Platters caught up, they'd been driving 3 hours more than than the Platters. xiii + three is 16, and then we know the Hills had been driving 16 hours by the time the Platters caught up with them.

	distance	rate	fourth dimension
the Hills	d	r	sixteen
the Platters	d	r + xv	13

Our chart gives united states two equations. The Hill family's trip can be described by d = r ⋅ 16. The equation for the Platter family's trip is d = (r + fifteen) ⋅ 13. Just similar with our other bug, we can combine these equations by replacing a variable in one of them.

The Hill family unit equation already has the value of d equal to r ⋅ xvi. So we'll supersede the d in the Platter equation with r ⋅ 16. This manner, it will be an equation we tin solve.

r ⋅ 16 = (r + 15) ⋅ thirteen

First, let's simplify the right side: r ⋅ 16 is sixteenr .

16r = (r + 15) ⋅ thirteen

Side by side, we'll simplify the correct side and multiply (r + 15) past 13.

16r = 13r + 195

We can become both r and their coefficients on the left side past subtracting thirteenr from 16r : 16r - 13r is 3r .

3r = 195

Now all that'southward left to exercise is get rid of the iii next to the r. To do this, we'll split up both sides past 3: 195 / 3 is 65.

r = 65

So at that place'south our answer: r = 65. The Hill family drove an average of 65 mph.

Y'all tin solve any overtaking problem the same manner we solved this i. Just recollect to pay special attention when y'all're setting upward your chart. But like the Hill family unit did in this problem, the person or vehicle who started moving first will e'er have a greater travel time.

Practice problem 2

Try solving this problem. It's similar to the trouble we only solved. When yous're finished, roll down to see the answer and an explanation.

A railroad train moving 60 mph leaves the station at apex. An hour later, a train moving 80 mph leaves heading the same management on a parallel track. What time does the second train grab upwardly to the first?

Problem 2 answer

Hither's practice problem two:

A railroad train moving sixty mph leaves the station at noon. An hr later, a train moving 80 mph leaves heading the same direction on a parallel rails. What time does the second train catch upwardly to the get-go?

Answer: 4 p.m.

To solve this trouble, start by making a chart. Hither'due south how it should expect:

	distance	rate	fourth dimension
fast train	d	80	t
slow train	d	sixty	t + 1

Here's an explanation of the chart:

• Distance: Both trains volition have traveled the aforementioned distance by the time the fast railroad train catches up with the tedious i, and so the distance for both is d .
• Charge per unit: The problem tells us how fast each train was going. The fast railroad train has a rate of 80 mph, and the wearisome train has a rate of 60 mph.
• Time: Nosotros'll use t to stand for the fast train's travel time before information technology catches up. Because the slow train started an hour before the fast ane, it will take been traveling i hr more by the fourth dimension the fast train catches up. Information technology's t + 1.

Now we have two equations. The equation for the fast train is d = 80t . The equation for the slow train is d = sixty (t + 1). To solve this problem, we'll need to combine the equations.

The equation for the fast railroad train says d is equal to eightyt . This means we tin can combine the two equations past replacing the d in the slow train's equation with 80t .

80t = 60 (t + 1)

First, let'southward simplify the right side of the equation: sixty ⋅ (t + one) is sixtyt + lx.

80t = 60t + lx

To solve the equation, nosotros'll accept to get t on one side of the equals sign and a number on the other. Nosotros can get rid of sixtyt on the right side past subtracting 60t from both sides: 80t - 60t is xxt .

20t = 60

Finally, we tin can get rid of the 20 adjacent to t by dividing both sides past twenty. 60 divided by 20 is 3.

t = 3

And then t is equal to three. The fast train traveled for 3 hours. Even so, it's not the answer to our problem. Allow'due south look at the original trouble over again. Pay attention to the last sentence, which is the question we're trying to answer.

A train moving sixty mph leaves the station at apex. An hour later, a train moving fourscore mph leaves heading the same direction on a parallel track. What fourth dimension does the 2d train catch up to the first?

Our trouble doesn't enquire how long either of the trains traveled. It asks what time the 2d train catches upward with the offset.

The problem tells us that the slow train left at apex and the fast one left an hour after. This means the fast train left at one p.m. From our equations, we know the fast train traveled 3 hours. 1 + 3 is 4, and so the fast train caught up with the slow one at four p.chiliad. The answer to the problem is iv p.thousand.

stichwhipar1984.blogspot.com

Source: https://edu.gcfglobal.org/en/algebra-topics/distance-word-problems/1/

Share this post